数据结构与算法学习
数据结构与算法
初识算法
算法
算法Algorithm是在有限时间内解决特定问题的一组指令或操作步骤
- 明确性:清晰输入输出
- 可行性:有限步骤、时间和内存空间下完成
- 结果确定性:相同的输入和运行下,输出相同
数据结构
数据结构 Data Structure计算机组织和存储数据的方式
- 空间占用尽量减少,节省计算机内存
- 数据操作尽可能快速,涵盖数据访问、添加、删除、更新等
- 提供简洁的数据表示和逻辑信息,以便使得算法高效运行
数据结构与算法关系
- 数据结构是算法的基石。数据结构为算法提供结构化存储的数据,以及用于操作数据的方法
- 算法对数据结构结构化存储的数据进行操作。数据结构本身仅存储数据信息,需要结合算法才能解决特定问题
- 特定算法通常有对应最优的数据结构。算法通常可以基于不同的数据结构进行实现,但最终执行效率可能相差很大
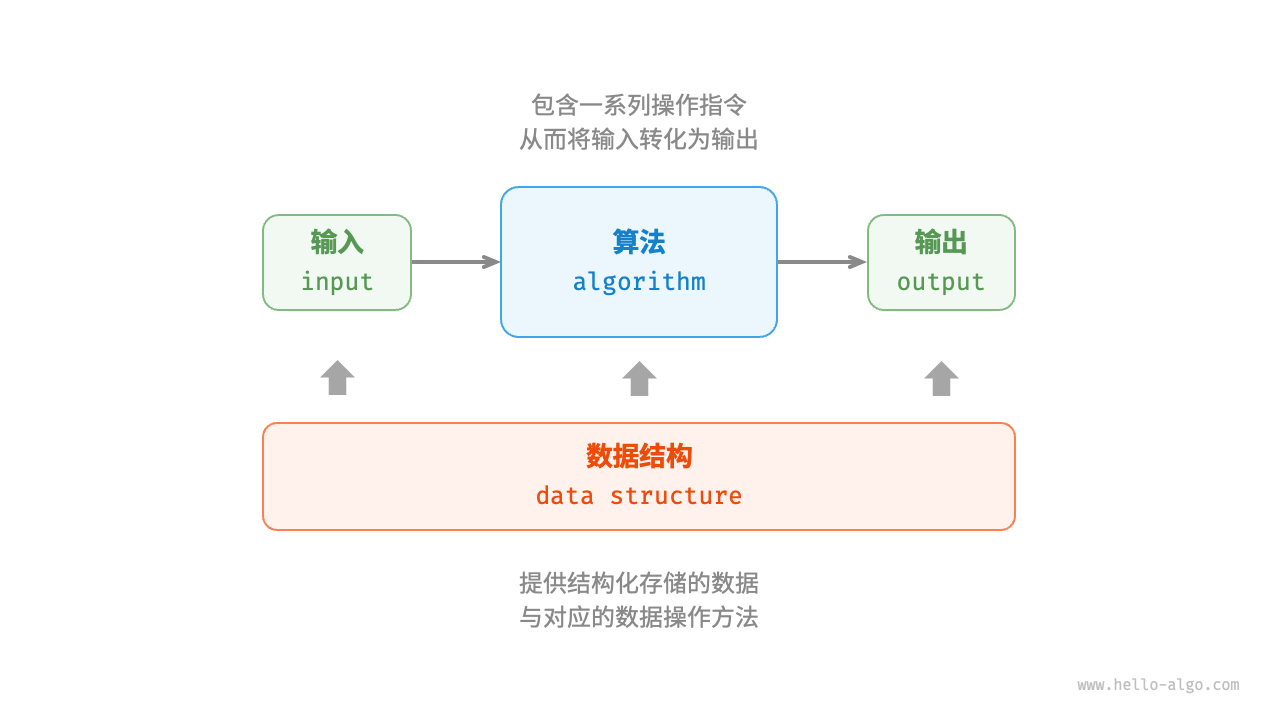
数据结构就类似于积木组织形成,包括形状、大小、连接方式等。算法就是把积木拼成最终形态的一系列操作步骤。积木对应于数据,积木形状和连接方式代表数据结构,拼装积木的步骤则对应算法
复杂度
算法设计追求层面
- 找到问题解法:算法需要在规定的输入范围内,可靠的求得问题的正确解
- 寻找最优解法:同一个问题可能存在多种解法,我们希望能够找到尽可能高效的算法
在解决问题的前提下,算法效率成为主要评价维度:
- 时间效率
- 空间效率
时间复杂度
常见类型
O(1) < O(\log n) < O(n) < O(n \log n) < O(n^2) < O(2^n) < O(n!)
{常数阶} < {对数阶} < {线性阶} < {线性对数阶} < {平方阶} < {指数阶} < {阶乘阶}
- 常数阶(O(1))
1
2
3
4
5
6
7
8/* 常数阶 */
int constant(int n) {
int count = 0;
int size = 100000;
for (int i = 0; i < size; i++)
count++;
return count;
} - 线性阶(O(n))
线性阶的操作数量相对于输入数据大小以线性级别增长。线性阶通常出现在单层循环中1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17/* 线性阶 */
int linear(int n) {
int count = 0;
for (int i = 0; i < n; i++)
count++;
return count;
}
/* 线性阶(遍历数组) */
int arrayTraversal(int[] nums) {
int count = 0;
// 循环次数与数组长度成正比
for (int num : nums) {
count++;
}
return count;
} - 平方阶(O(n^2))
平方阶的操作数量相对于输入数据大小以平方级别增长。平方阶通常出现在嵌套循环中,外层循环和内层循环都为 (O(n)) ,因此总体为 (O(n^2)) 。以「冒泡排序」为例,外层循环执行 (n - 1) 次,内层循环执行 (n-1, n-2, …, 2, 1) 次,平均为 (\frac{n}{2}) 次,因此时间复杂度为 (O(n^2)) 。1
2
3
4
5
6
7
8
9
10
11/* 平方阶 */
int quadratic(int n) {
int count = 0;
// 循环次数与数组长度成平方关系
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
count++;
}
}
return count;
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18/* 平方阶(冒泡排序) */
int bubbleSort(int[] nums) {
int count = 0; // 计数器
// 外循环:未排序区间为 [0, i]
for (int i = nums.length - 1; i > 0; i--) {
// 内循环:将未排序区间 [0, i] 中的最大元素交换至该区间的最右端
for (int j = 0; j < i; j++) {
if (nums[j] > nums[j + 1]) {
// 交换 nums[j] 与 nums[j + 1]
int tmp = nums[j];
nums[j] = nums[j + 1];
nums[j + 1] = tmp;
count += 3; // 元素交换包含 3 个单元操作
}
}
}
return count;
} 指数阶(O(2^N))
生物学的“细胞分裂”是指数阶增长的典型例子:初始状态为 (1) 个细胞,分裂一轮后变为 (2) 个,分裂两轮后变为 (4) 个,以此类推,分裂 (n) 轮后有 (2^n) 个细胞。1
2
3
4
5
6
7
8
9
10
11
12
13/* 指数阶(循环实现) */
int exponential(int n) {
int count = 0, base = 1;
// 细胞每轮一分为二,形成数列 1, 2, 4, 8, ..., 2^(n-1)
for (int i = 0; i < n; i++) {
for (int j = 0; j < base; j++) {
count++;
}
base *= 2;
}
// count = 1 + 2 + 4 + 8 + .. + 2^(n-1) = 2^n - 1
return count;
}在实际算法中,指数阶常出现于递归函数。例如以下代码,其递归地一分为二,经过 (n) 次分裂后停止。
1
2
3
4
5
6/* 指数阶(递归实现) */
int expRecur(int n) {
if (n == 1)
return 1;
return expRecur(n - 1) + expRecur(n - 1) + 1;
}指数阶增长非常迅速,在穷举法(暴力搜索、回溯等)中比较常见。对于数据规模较大的问题,指数阶是不可接受的,通常需要使用动态规划或贪心等算法来解决。
对数阶(O(logn))
与指数阶相反,对数阶反映了“每轮缩减到一半”的情况。设输入数据大小为 (n) ,由于每轮缩减到一半,因此循环次数是 (log2n) ,即 (2^n) 的反函数。1
2
3
4
5
6
7
8
9/* 对数阶(循环实现) */
int logarithmic(float n) {
int count = 0;
while (n > 1) {
n = n / 2;
count++;
}
return count;
}与指数阶类似,对数阶也常出现于递归函数。以下代码形成了一个高度为 (log2n) 的递归树。
1
2
3
4
5
6/* 对数阶(递归实现) */
int logRecur(float n) {
if (n <= 1)
return 0;
return logRecur(n / 2) + 1;
}线性对数阶(O(n\logn))
线性对数阶常出现于嵌套循环中,两层循环的时间复杂度分别为 (O(\log n)) 和 (O(n)) 。
主流排序算法的时间复杂度通常为 (O(n \log n)) ,例如快速排序、归并排序、堆排序等。1
2
3
4
5
6
7
8
9
10
11/* 线性对数阶 */
int linearLogRecur(float n) {
if (n <= 1)
return 1;
int count = linearLogRecur(n / 2) +
linearLogRecur(n / 2);
for (int i = 0; i < n; i++) {
count++;
}
return count;
}
- 阶乘阶(O(n!))
阶乘通常使用递归实现。例如以下代码,第一层分裂出 (n) 个,第二层分裂出 (n - 1) 个,以此类推,直至第 (n) 层时终止分裂。1
2
3
4
5
6
7
8
9
10
11/* 阶乘阶(递归实现) */
int factorialRecur(int n) {
if (n == 0)
return 1;
int count = 0;
// 从 1 个分裂出 n 个
for (int i = 0; i < n; i++) {
count += factorialRecur(n - 1);
}
return count;
}
空间复杂度
算法运行过程中使用的内存空间主要包括以下几种:
- 输入空间:用于存储算法的输入数据。
- 暂存空间:用于存储算法运行过程中的变量、对象、函数上下文等数据。
- 输出空间:用于存储算法的输出数据。
一般情况下,空间复杂度的统计范围是暂存空间加上输出空间。
暂存空间可以进一步划分为三个部分:
- 暂存数据:用于保存算法运行过程中的各种常量、变量、对象等。
- 栈帧空间:用于保存调用函数的上下文数据。系统在每次调用函数时都会在栈顶部创建一个栈帧,函数返回后,栈帧空间会被释放。
- 指令空间:用于保存编译后的程序指令,在实际统计中通常忽略不计。
因此在分析一段程序的空间复杂度时,我们通常统计暂存数据、输出数据、栈帧空间三部分。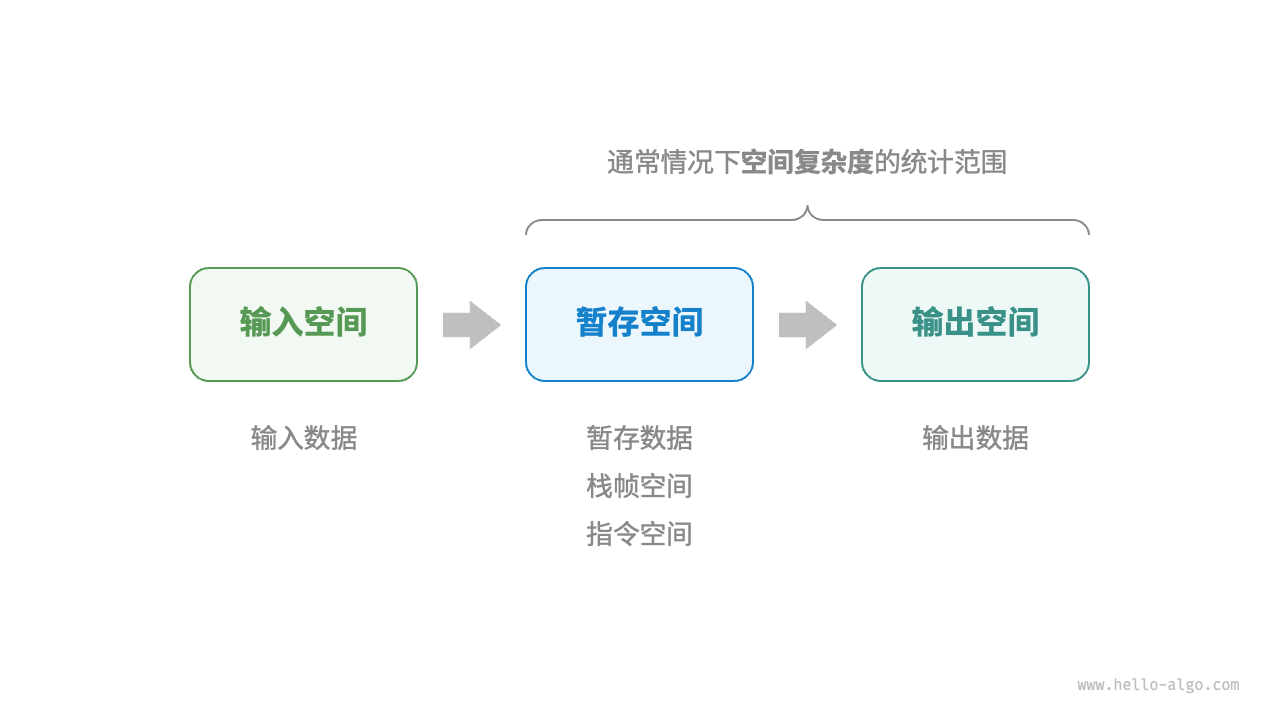
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20/* 类 */
class Node {
int val;
Node next;
Node(int x) { val = x; }
}
/* 函数 */
int function() {
// do something...
return 0;
}
int algorithm(int n) { // 输入数据
final int a = 0; // 暂存数据(常量)
int b = 0; // 暂存数据(变量)
Node node = new Node(0); // 暂存数据(对象)
int c = function(); // 栈帧空间(调用函数)
return a + b + c; // 输出数据
}我们通常只关注「最差空间复杂度」
常见的空间复杂度类型有(从低到高排列):
O(1) < O(\log n) < O(n) < O(n^2) < O(2^n)
{常数阶} < {对数阶} < {线性阶} < {平方阶} < {指数阶}
数据结构
逻辑结构
逻辑结构是数据元素之间的逻辑关系
- 线性数据结构:数组、链表、栈、队列、哈希表
- 非线性数据结构:树、堆、图、哈希表
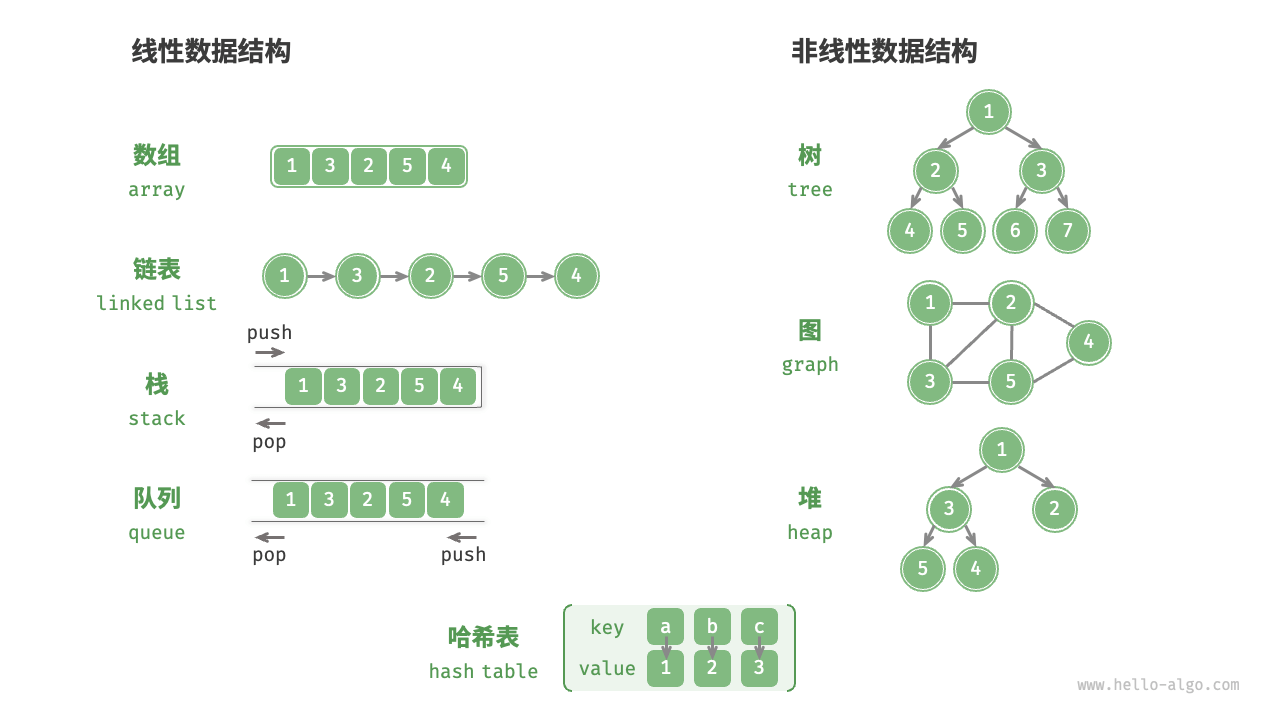
非线性数据结构可以进一步被划分为树形结构与网状结构
- 线性结构:数组、链表、队列、栈、哈希表,元素存在一对一的顺序关系。
- 树形结构:树、堆、哈希表,元素存在一对多的关系。
- 网状结构:图,元素存在多对多的关系。
- 基于数组可实现:栈、队列、哈希表、树、堆、图、矩阵等。
- 基于链表可实现:栈、队列、哈希表、树、堆、图等。
数字编码
原码,反码,补码
- 原码:我们将数字的二进制表示的最高位视为符号位,其中 (0) 表示正数,(1) 表示负数,其余位表示数字的值。
- 反码:正数的反码与其原码相同,负数的反码是对其原码除符号位外的所有位取反。
- 补码:正数的补码与其原码相同,负数的补码是在其反码的基础上加 (1) 。
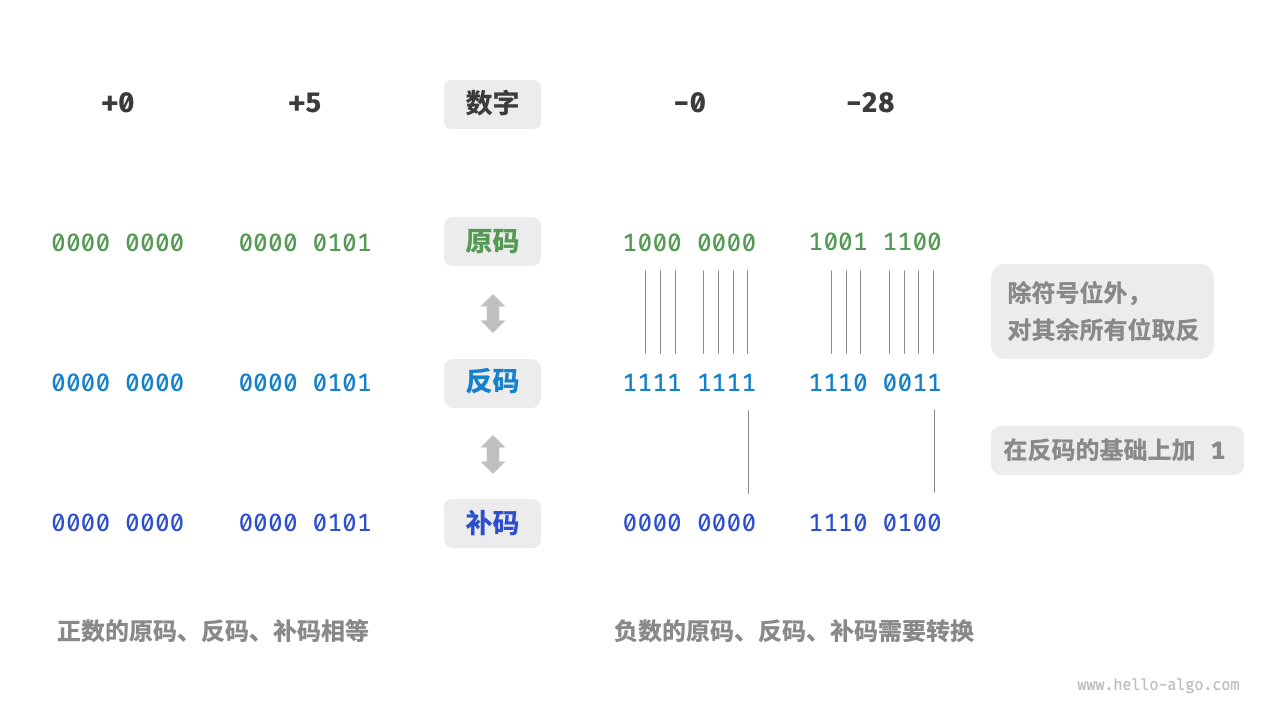
然而数字却是以「补码」的形式存储在计算机中的
这是因为原码存在一些局限性。
一方面,负数的原码不能直接用于运算。例如,我们在原码下计算 (1 + (-2)) ,得到的结果是 (-3) ,这显然是不对的。
为了解决此问题,计算机引入了「反码」。例如,我们先将原码转换为反码,并在反码下计算 (1 + (-2)) ,并将结果从反码转化回原码,则可得到正确结果 (-1) 。
另一方面,数字零的原码有 (+0) 和 (-0) 两种表示方式。这意味着数字零对应着两个不同的二进制编码,而这可能会带来歧义问题。例如,在条件判断中,如果没有区分正零和负零,可能会导致错误的判断结果。如果我们想要处理正零和负零歧义,则需要引入额外的判断操作,其可能会降低计算机的运算效率。